Поверхностный интеграл 1 рода. Вычисление поверхностных интегралов: теория и примеры. МА. Поверхностные интегралы второго рода

Пример 3.3. Вычислить работу векторного поля

a = 2x 2 yi – xy 2 j

от начала координат O до точки A(1;1), если движение происходит вдоль: а) отрезка прямой ; б) дуги параболы ; в) ломаной OBA, где B(1;0) (см. рис. 3.1).

Решение . а) Уравнение прямой OA имеет вид y=x . Пусть x=t , тогда уравнение прямой в параметрическом виде примет вид:

x=t, y=t,

причем при движении от A до B параметр t будет меняться от 0 до 1. Тогда совершенная работа будет равна

б) Пусть x=t 2 , y=t , тогда

x=t 2 , y=t, 0£t £1.

.

в) Уравнение прямой (OB) имеет вид y =0 (0£x £1); уравнение прямой (BA) имеет вид x =1 (0£y £1). Тогда

, .

В результате, получаем,

.

Замечание . Если в случае двухмерных полей уравнение линии описывается уравнением y =y (x ), а переменная x изменяется от a до b , то криволинейный интеграл 2-го будет вычисляться по формуле:

. (3.9)

Предыдущий пример можно было бы решить и при помощи этой формулы, не вводя параметр t .

Пример 3.4. Вычислить интеграл

,

где L – дуга параболы y=x 2 +1 от точки A(0;1) до точки B(2;5).

Решение . Сделаем чертеж (см. рис.3.2). Из уравнения параболы получаем y"=2x . Поскольку на дуге параболы AB переменная x изменяется от 0 до 2, то криволинейный интеграл, в соответствии с формулой (3.9), примет вид

4. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ

4.1. Поверхностные интегралы первого рода

Поверхностный интеграл 1-го рода является обобщением двойного интеграла и вводится аналогичным образом. Рассмотрим некоторую поверхность S , гладкую или кусочно-гладкую, и предположим, что функция f(x,y,z ) определена и ограничена на этой поверхности. Разобьем эту поверхность на n произвольных частей. Площадь каждого участка обозначим через Ds i . На каждом участке выберем какую-либо точку с координатами (x i ,y i ,z i ) и вычислим значение функции в каждой такой точке. После этого составим интегральную сумму:

.

Если существует предел интегральных сумм при n ®¥ (при этом max Ds i ®0), т.е. такой предел не зависит ни от способа разбиения, ни от выбора средних точек, то такой предел называется поверхностным интегралом первого рода :

. (4.1)

Если функция f(x,y,z ) непрерывна на поверхности S , то предел (4.1) существует.

Если подынтегральная функция f(x,y,z )º1, то поверхностный интеграл 1-го рода равен площади поверхности S :

. (4.2)

Допустим, что введена декартова система координат, и любая прямая, параллельная оси Oz, может пересекать поверхность S лишь в одной точке. Тогда уравнение поверхности S можно записать в виде

z = z (x,y )

и она однозначно проецируется на плоскость xOy . В результате поверхностный интеграл 1-го рода можно выразить через двойной интеграл

. (4.3)

Пример 4.1. Вычислить интеграл

,

где S – часть конической поверхности z 2 =x 2 +y 2 , 0£z £1.

Решение. Имеем

Тогда искомый интеграл преобразуется в двойной интеграл

где S xy – круг x 2 +y 2 £1. Поэтому

.

4.2. Поверхностные интегралы второго рода

Пусть в некоторой области задано векторное поле

a = a x i + a y j + a z k

и какая-либо двухсторонняя поверхность S . Разобьем поверхность каким-либо способом на элементарные площадки DS i . На каждой площадке выберем произвольную точку P i и составим интегральную сумму:

, (4.4)

где n (P i ) – вектор нормали к заданной поверхности в точке P i . Если существует предел такой суммы при DS i ®0, то этот предел называется поверхностным интегралом 2-го рода (или потоком векторного поля a через поверхность S ) и обозначается символом

или ,

где ds =n ds .

Поскольку единичный вектор нормали имеет своими координатами направляющиеся косинусы n ={cosa, cosb, cosg}. то

Таким образом, вычисление поверхностных интегралов 2-го рода можно свести к вычислению поверхностных интегралов 1-го рода. Однако, что в отличие от поверхностных интегралов 1-го рода интегралы 2-го рода зависят от выбора стороны поверхности. Переход к другой стороне поверхности меняет направление нормали к поверхности, а соответственно и знак интеграла .

Рассмотрим интеграл

.

Пусть уравнение поверхности имеет вид z =j(x,y ) и положительной стороной этой поверхности будем считать ту, нормаль которой образует с осью Oz острый угол. Тогда

cosgds = dxdy.

Поэтому рассматриваемый интеграл можно записать в виде

.

Заменяя z на j(x,y ), придем к двойному интегралу

,

где S xy – проекция поверхности S на плоскость xOy .

Теоретический минимум

Эта тема продолжает обсуждение криволинейных и поверхностных интегралов, начатое в теме " ". Рекомендуется предварительно ознакомиться с той темой. Ввиду большей сложности темы криволинейные и поверхностные интегралы
второго рода рассматриваются отдельно. Здесь обсуждаются поверхностные интегралы второго рода - пожалуй, наиболее сложная интегральная операция в
анализе функций многих переменных. План будет совершенно аналогичен рассмотрению криволинейного интеграла второго рода. Начнём с физических приложений,
а потом уже перейдём к формальному математическому аспекту.

1. Физические приложения поверхностного интеграла второго рода

Самый естественный способ ввести поверхностный интеграл второго рода - рассмотреть поток жидкости через некоторую поверхность. Начнём с простого случая:
жидкость течёт вдоль оси абсцисс с постоянной скоростью . Выделим перпендикулярную течению площадку и найдём массу жидкости, проходящую через
неё за время . За это время через площадку проходит «параллелепипед» высотой и с основанием площадью . Масса этого «параллелепипеда»
равна , где - плотность жидкости.

Теперь пусть жидкость течёт параллельно плоскости под углом к оси абсцисс, но по-прежнему со скоростью . Площадку из предыдущего
случая расположим по-прежнему перпендикулярно оси абсцисс. За время через неё проходит наклонный «параллелепипед» (см. рис. 1). Его масса
равна . Заметим, что введение единичного вектора нормали к площадке позволяет записать .
Вводится формальный вектор элементарной площадки , модуль которого равен , а его направление совпадает с направлением вектора
нормали к площадке. Тогда . Такая запись позволяет не заботиться о направлении вектора скорости жидкости по отношению
к площадке.

Осталось отказаться от малости площадки, через которую течёт жидкость, и от предположение о постоянстве модуля и направления скорости. Тогда
поверхность разбивается на малые части, в пределах которой вектор скорости можно считать постоянным. Масса жидкости, проходящей через поверхность,
приближённо даётся суммой
.
Точная формула получится в пределе разбиения поверхности на бесконечно малые части. Предел является поверхностным интегралом второго рода:
.
При написании этого раздела использован фрагмент учебного материала преподавателя кафедры общей физики, используемый им на семинарских занятиях.

2. Определение поверхностного интеграла второго рода

Теперь о формальном построении интеграла. В связи с тем, что интегрируется по поверхности векторное поле, имеет смысл уточнять, по какой стороне
поверхности вычисляется интеграл (как при вычислении потока жидкости: втекает жидкость внутрь поверхности или вытекает из неё). Поэтому особо уточняется,
что поверхность, по которой проводится интегрирование, должна быть двусторонней или ориентируемой (т.е. лист Мёбиуса как целое не подойдёт). Поверхность
сразу ориентируется, т.е. выбирается определённое направление нормали к поверхности (скажем, если интеграл вычисляется по сфере, то нормаль может быть
направлена из сферы или внутрь сферы). Компоненты поля являются в общей случае функциями точки. Поверхность интегрирования
разбивается на малые части , в каждой части выбирается точка и составляется сумма
,
где - площадь проекции элемента на плоскость , - площадь проекции этого элемента на плоскость , - площадь
проекции этого элемента на плоскость . Проводим суммированием по всем элементам, на которые разбита поверхность:

и переходим к пределу, устремляя к нулю диаметр наибольшей частичной области. Предел является поверхностным интегралом второго рода
.

Покажем, как привести этот интеграл к виду из п.1. Для этого придётся сделать небольшое отступление чисто геометрического характера. Пусть имеется
плоскость , пересекающая оси координат (см. рис. 2). Часть этой плоскости, расположенная в первом октанте, имеет площадь . Требуется найти площади
всех трёх ортогональных проекций данной части плоскости на координатные плоскости. Как известно, площадь проекции фигуры равна произведению площади
самой фигуры и косинуса угла между плоскостью фигуры и плоскостью, на которую она проектируется (см. рис. 3). Т.е. нужно найти углы, которые составляет
плоскость с координатными плоскостями. Угол между двумя плоскостями равен углу между их нормалями. Единичная нормаль к плоскости имеет компоненты,
являющиеся её направляющими косинусами. Поэтому угол между плоскостью и плоскостью равен (см. рис. 2), а значит .
Это же соотношение будет справедливо для бесконечно малых площадок: . И аналогично .
С учётом этих соотношений интеграл примет вид
.
Кстати, эта форма записи более наглядна, поэтому работать будем именно с ней.

Изменение направления нормали на противоположное приводит к тому, что интеграл меняет знак.

3. Вычисление поверхностного интеграла второго рода

После приведения интеграла к форме, содержащей направляющие косинусы нормали к поверхности, задача по сути сводится к записи единичной нормали
с дальнейшим вычислением поверхностного интеграла первого рода. В этих действиях есть некоторая специфика, поэтому подробно разберёмся с вычислением
интегралов такого типа.

Начнём со случая, когда поверхность интегрирования задана явным уравнением, например, . Тогда вектор нормали записывается так:
,
а элемент площади поверхности
.
В результате поверхностный интеграл принимает следующий вид:
, (1)
где - область плоскости , в которую проектируется поверхность интегрирования.

Может быть так, что поверхность интегрирования правильно проектируется на плоскость (и задаётся уравнением ) или на плоскость
(и задаётся уравнением ). Тогда формула, по которой вычисляется интеграл, немного корректируется:
(2)
или
. (3)
Конечно, запоминать такие формулы не рекомендуется: легко что-нибудь перепутать - лучше восстанавливать их применительно к конкретному
расчёту заново, исходя из формулы для вектора нормали и площади малого элемента поверхности.

Есть один выделенный случай, когда поверхность правильно проектируется на все три координатные плоскости, т.е. из уравнения поверхности любая переменная
может быть выражена однозначно. Тогда расчёт существенно упрощается. Обратите внимание на структуру формул (1) - (3). В каждой из них можно выделить три
слагаемых, причём одно из них выглядит проще других. При проектировании поверхности на плоскость это слагаемое, содержащее компоненту
поля ; при проектировании на плоскость это слагаемое, содержащее компоненту ; при проектировании на плоскость это слагаемое,
содержащее компоненту . Если поверхность правильно проектируется на любую координатную плоскость, то мы разобьём интеграл
на три части и спроектируем каждую часть наиболее удобным способом:
.

Наконец, случай параметрического задания поверхности
.
Как и при вычислении поверхностного интеграла первого рода, нужно считать три якобиана:
.
Через них выражаются направляющие косинусы нормали:
,
элемент поверхности
.
Таким образом, для интеграла получаем
,
где - область изменения параметров, соответствующая поверхности интегрирования.

4. Формула Стокса. Формула Остроградского-Гаусса

С поверхностным интегралом второго рода связаны две формулы, находящие разнообразные применения, в том числе в физических приложениях.
Формула Стокса:
,
где ,
поверхность натянута на контур , обход контура согласован с выбором нормали к поверхности по правилу правого винта.
Уточнения требуются, если поверхность интегрирования имеет "дырки".
Формула Грина является частным случаем этой формулы. Кроме того, из формулы Стокса следует условие независимости криволинейного интеграла второго
рода от формы пути.

Формула Остроградского-Гаусса.
Для векторного поля выполняется формула

где поверхность ограничивает объём .

Формула Остроградского-Гаусса имеет разные применения. Остановимся на двух из них. Во-первых, легко доказать, что объём тела может быть вычислен
по формуле

Во-вторых, иногда бывает необходимо вычислить поверхностный интеграл второго рода по незамкнутой поверхности, связанный с громоздким расчётом.
Тогда поверхность замыкают, преобразуют интеграл к тройному и вычитают интеграл по добавленной поверхности (см. пример ниже).

Замечание . Формулы Стокса и Остроградского-Гаусса удобнее записываются в векторном анализе с использованием ротора и дивергенции векторного поля.

Примеры вычисления поверхностных интегралов второго рода

Пример 1. Интеграл по плоскости .. Тогда получим) части эллиптического параболоида (нормаль внешняя).

Перепишем интеграл в виде
.
Поверхность иинтегрирования - эллиптический параболоид - правильно проектируется только на плоскость , поэтому записываем уравнение поверхности в виде
.
Находим единичный вектор нормали:
.

На случаи, когда интегрирование происходит не по отрезку кривой, а по ограниченной поверхности. Как и криволинейные интегралы, поверхностные интегралы бывают первого рода и второго рода.

Поверхностный интеграл первого рода записывается в виде

где f (M ) = f (x,y,z ) – функция трёх переменных, а поверхность σ - область интегрирования этой функции. Если f (x,y,z ) равна единице, то поверхностный интеграл равен площади поверхности.

Представьте себе довольно большой подсолнух с очень-очень маленькими семечками. Тогда по сумме поверхностей очень-очень маленьких семечек, расположенных на поверхности подсолнуха, можно вычислить поверхность подсолнуха - таким может быть упрощённое толкование поверхностного интеграла. Почему так?

Давайте перейдём к более формальному определению поверхностного интеграла. Поверхность σ разбита на n частей с площадями Δσ 1 , Δσ 2 , ..., Δσ n . Если выбрать на каждой частичной поверхности (семечке) произвольную точку M i с координатами (ζ i , η i , ς i ,) , то можно составить сумму

Эта сумма называется интегральной суммой для функции f (M ) по поверхности σ . Теперь будем максимально увеличивать число таких маленьких частей, а наибольший диаметр Δσ i - наоборот, уменьшать. Если интегральная сумма при стремлении наибольшего из диаметров частей к нулю (то есть, как мы уже отмечали, все части очень маленькие) имеет предел, то этот предел и называется поверхностным интегралом первого рода от функции f (M ) по поверхности σ .

Вычисление поверхностного интеграла первого рода

Пусть поверхность σ задана уравнением z = z (x , y ) , её проекцией на плоскость xOy является область D xy , при этом функция z = z (x , y ) и её частные производные и непрерывны в области D xy .

Пример 1.

где σ - часть плоскости в первом октанте.

Решение. Чертёж:

Из уравнения плоскости получаем выражение "зет": .

Тогда частные производные: , и

.

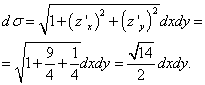Поверхность σ является изображённым на чертеже треугольником ABC , а его проекцией на плоскость xOy - треугольником AOB , который ограничен прямыми x = 0 , y = 0 и 3x + y = 6 . От поверхностного интеграла перейдём к двойному интегралу и решим его:

.

Понятие поверхностного интеграла второго рода

Прежде чем перейти к определению поверхностного интеграла второго рода, требуется познакомиться с понятиями стороны поверхностей и ориентированных поверхностей.

Пусть в пространстве дана гладкая поверхность σ . На этой поверхности выберем произвольную точку M и проведём через неё вектор нормали к поверхности. Через точку M проведём также на поверхности σ произвольный контур, не имеющий общих точек с границей поверхности σ . Точку M вместе с вектором нормали будем перемещать по контуру так, чтобы вектор нормали постоянно был перпендикулярен поверхности σ . По возвращении точки M в начальное положение возможны два случая: направление вектора нормали сохранится или же поменяется на противоположное.

Если направление вектора нормали не поменяется, то поверхность σ называется двусторонней. Если же при обходе контура направление вектора нормали поменяется на противоположное, то поверхность называется односторонней. Двусторонние поверхности называются ориентированными поверхностями, односторонние - неориентированными поверхностями.

Пример односторонней поверхности - лист Мёбиуса (на рисунке выше), который можно сделать из полоски бумаги, одна сторона которой повёрнута на 180 градусов, и затем концы склеены. И вот что здесь важно: для односторонней поверхности понятие поверхностного интеграла второго рода не вводится .

Так что будем рассматривать только двусторонние поверхности. Примеры двусторонних поверхностей - плоскости, сфера, эллипсоил, параболоид.

Положительную сторону двустороней поверхности определяет направление вектора нормали. Противоположная сторона поверхности называется отрицательной. Положительной стороной поверхности называется её верхняя сторона. Если единичные векторы нормали составляют острые углы с осью Oz , то выбрана верхняя сторона поверхности z = z (x , y ) , если углы тупые, то нижняя сторона поверхности.

Как и в случае поверхностного интеграла первого рода, поверхность можно разбить на n частей. При формулировке понятия поверхностного интеграла первого рода в интегральной сумме присутствовали площади каждой из частей, на которые умножаются значения функции f (M i ) . В случае поверхностного интеграла второго рода берутся площади не самих частей, а площади их проекций на координатные плоскости . А функцию трёх переменных для отличия от интеграла первого рода обозначим R (x ,y ,z ) . Тогда интегральная сумма запишется так:

,

где Δs i - площади упомянутых проекций частей стороны поверхности на координатную ось (пока будем считать, что на ось xOy ).

При таких соглашениях и обозначениях определение поверхностного интеграла второго рода аналогично определению интеграла первого рода. А именно: поверхностным интегралом второго рода называется предел данной интегральной суммы при стремлении к нулю наибольшего из диаметров частей рассматриваемой поверхности.

Записывается он так:

.

В данном случае функция R (x ,y ,z ) интегрируема по переменным x и y , так как части поверхности проецировались на плоскость xOy .

Аналогично можно записать и два других поверхностных интеграла второго рода:

(функция P (x ,y ,z ) интегрируема по переменным y и z yOz ),

(функция Q (x ,y ,z ) интегрируема по переменным z и x , так как части поверхности проецируются на плоскость zOx ).

Сумма этих интегралов

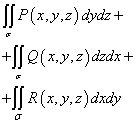
называется общим поверхностным интегралом второго рода и обозначается

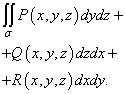
Вычисление поверхностного интеграла второго рода

Поверхностный интеграл второго рода вычисляется путём разложения общего поверхностного интеграла второго рода на сумму поверхностных интегралов (см. окончание предыдущего параграфа) и сведением каждого из них к двойному интегралу.

Рассмотрим подробно вычисление интеграла

.

Пусть поверхность σ задана уравнением z = z (x , y ) . Положительную сторону поверхности обозначим , отрицателную , а проекцию на плоскость xOy - D xy .

Таким образом, получаем формулу для вычисления поверхностного интеграла второго рода:

Если выбрана отрицательная сторона поверхности, то знак интеграла меняется:

Аналогично вычисляются два других отдельных интеграла - слагаемых общего:

Пример 2.

,

где σ - верхняя сторона части плоскости , отсечённая плоскостями y = 0 и y = 4 и находящаяся в первом октанте.

Решение. Чертёж - на рисунке сверху. По определению получаем сумму трёх двойных интегралов:

Второй интеграл равен нулю, так как плоскость σ параллельна оси Oy . Поэтому найдём первый и третий интегралы:

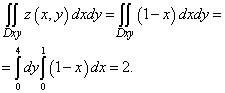
Остаётся лишь сложить все отдельные интегралы и получить общий поверхностный интеграл второго рода:

.

Если требуется вычислить поверхностный интеграл второго рода по замкнутой поверхности, можно перейти к тройному интегралу , используя формулу Остроградского. Тогда, если функции P (x,y,z ) , Q (x,y,z ) и R (x,y,z ) и их частные производные , , - непрерывные функции в области W , которую ограничивает замкнутая поверхность σ , то при интегрировании по внешней стороне поверхности в силе равенство

Пример 3. Вычислить поверхностный интеграл второго рода

,

где σ - внешняя сторона поверхности конуса, образованного поверхностью и плоскостью z = 2 .

Решение. Данная поверхность является поверхностью конуса с радиусом R = 2 и высотой h = 2 . Это замкнутая поверхность, поэтому можно использовать формулу Остроградского. Так как P = 3x , Q = 4y , R = −z , то частные производные , , .

Переходим к тройному интегралу, который и решаем:

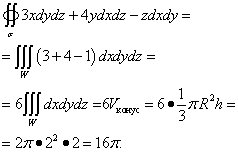
Больше примеров на вычисление поверхностных интегралов

Пример 4. Вычислить поверхностный интеграл первого рода

где σ - боковая поверхность конуса при .

Решение. Так как частные производные , , 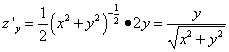то

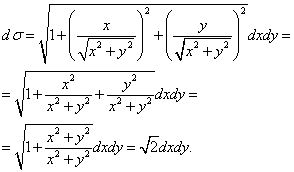
Сводим данный поверхностный интеграл к двойному:

Проекцией поверхности на плоскость xOy является круг с центром в начале координат и радиусом R = 2 , поэтому при вычислении двойного интеграла перейдём к полярной системе координат. Для этого сделаем замену переменных:

Получаем следующий интеграл, который окончательно и решаем:

Пример 5. Вычислить поверхностный интеграл второго рода

,

где σ - верхняя часть треугольника, образованного пересечением плоскости с координатными плоскостями.

Решение. Данный поверхностный интеграл разделим на сумму двух интегралов

, где

.

Чтобы вычислить интеграл I 1 σ на плоскость yOz . Проекцией является треугольник OCB , который на плоскости yOz ограничивают прямые или , y = 0 и z = 0 . Из уравнения плоскости выводится . Поэтому можем вычислить интеграл I 1 :

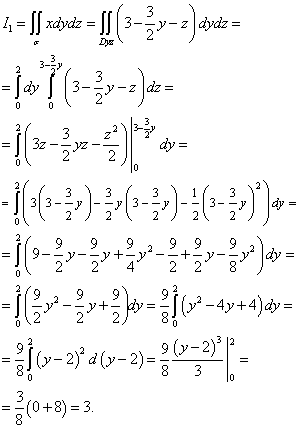
Чтобы вычислить интеграл I 2 , построим проекцию поверхности σ на плоскость zOx . Проекцией является треугольник AOC , который ограничивают прямые или , x = 0 и z = 0 . Вычисляем:

Складываем два полученных интеграла и окончательно получаем данный поверхностный интеграл:

.

Пример 6. Вычислить поверхностный интеграл второго рода

,

где σ - внешняя поверхность пирамиды, образованной плоскостью и координатными плоскостями.

Если при определении длины кривой она задавалась как предел вписанной в данную кривую ломаной при стремлении к нулю длины наибольшего ее отрезка, то попытка распространить это определение на площадь криволинейной поверхности может привести к противоречию (пример Шварца: можно рассмотреть последовательность вписанных в цилиндр многогранников, у которых наибольшее расстояние между точками какой-либо грани стремится к нулю, а площадь стремится к бесконечности). Поэтому определим площадь поверхности иным способом. Рассмотрим незамкнутую поверхность S, ограниченную контуром L, и разобьем ее какими-либо кривыми на части S1, S2,…, Sn. Выберем в каждой части точку Mi и спроектируем эту часть на касательную плоскость к поверхности, проходящую через эту точку. Получим в проек-ции плоскую фигуру с площадью Ti. Назовем ρ наибольшее расстояние между двумя точками любой части поверхности S.

Определение 12.1. Назовем площадью S поверхности предел суммы площадей Ti при

Поверхностный интеграл первого рода.

Рассмотрим некоторую поверхность S, ограниченную контуром L, и разобьем ее на части S1, S2,…, Sп (при этом площадь каждой части тоже обозначим Sп). Пусть в каждой точке этой поверхности задано значение функции f(x, y, z). Выберем в каждой части Si точку Mi (xi, yi, zi) и составим интегральную сумму

. (12.2)

Определение 12.2. Если существует конечный предел при интегральной суммы (12.2), не зависящий от способа разбиения поверхности на части и выбора точек Mi, то он называется поверхностным интегралом первого рода от функ-ции f(M) = f(x, y, z) по поверхности S и обозначается

Замечание. Поверхностный интеграл 1-го рода обладает обычными свойствами интегралов (линейность, суммирование интегралов от данной функции по отдельным частям рассматриваемой поверхности и т.д.).

Геометрический и физический смысл поверхностного интеграла 1-го рода.

Если подынтегральная функция f(M) ≡ 1, то из определения 12.2 следует, что равен площади рассматриваемой поверхности S.

Вычисление поверхностного интеграла 1-го рода.

Ограничимся случаем, когда поверхность S задается явным образом, то есть уравне-нием вида z = φ(x, y). При этом из определения площади поверхности следует, что

Si = , где Δσi - площадь проекции Si на плоскость Оху, а γi - угол между осью Oz и нормалью к поверхности S в точке Mi. Известно, что

,

где (xi, yi, zi) - координаты точки Mi. Cледовательно,

Подставляя это выражение в формулу (12.2), получим, что

,

где суммирование справа проводится по области Ω плоскости Оху, являющейся проекцией на эту плоскость поверхности S (рис.1).

При этом в правой части получена интегральная сумма для функции двух переменных по плоской области, которая в пределе при дает двойной интеграл Таким образом, получена формула, позволяющая свести вычисление поверхностного интеграла 1-го рода к вычислению двойного интеграла.